
Gridded Surface Construction from Points
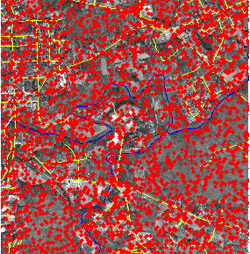
Input LIDAR points shown in red. For clarity, only one in every one hundred LIDAR points are shown. Region shown is a small area outside of Hillsborough, NC along the Eno river. | enlarge
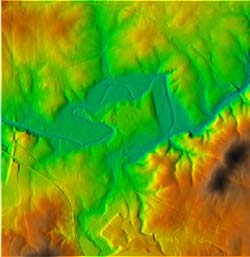
Corresponding DEM derived from LIDAR points with color representing height. Region shown is a small area outside of Hillsborough, NC along the Eno river. | enlarge
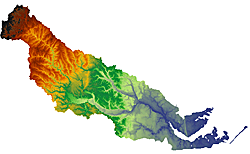
DEM of Neuse River basin in North Carolina derived from 390 million LIDAR points. | enlarge
Geographic Information Systems (GIS) often store representations of continuous surfaces representing physical properties such as elevation, temperature, water depth, etc., which can be approximated to a reasonable level of accuracy by smooth, single valued functions of the form z=F(x,y). Often such a surface is stored as a regular grid—or raster—of data values. When physically measuring the value of the surface, it is often impossible to collect data for every point on the surface. Instead, scientists collect a sample S of N spot measurements of the form (x,y,z) and reconstruct the continuous surface z=F(x,y) by interpolating the points in S.
We are particularly interested in data sets collected using LIDAR—a remote sensing method that collects highly accurate and dense point samples that measure the height of a terrain. Given a set S of N LIDAR points, we want to construct a gridded digital elevation model (DEM) of the terrain represented by S. Because LIDAR point sets are dense, and thousands of points can be collected in seconds, LIDAR data sets often consist of millions or billions of points. Processing such large point sets poses a number of computational challenges.
Issues
Many sophisticated point interpolation routines have been developed that solve a system of N linear equations given N input points. Because such methods do not scale to data sets containing more than a few hundred or a few thousand points, many methods rely on a segmentation scheme that decomposes the plane into a set of non-overlapping areas (or segments), containing a small number of points each. Each segment can then be interpolated independently but, to achieve smoothness across segment boundaries, it is necessary to use at least a subset of the points from neighboring segments in the interpolation. Often the segments are defined by the areas associated with the leaves of a quad-tree on the set of input points. For extremely large point sets common in LIDAR applications, not all input points can simultaneously reside in the main memory of a computer and must therefore reside on larger but much slower disks. In this case the transfer of data between disk and main memory (also called I/O), rather than computation, often becomes the performance bottleneck. Therefore we must consider I/O-efficient methods for constructing the segmentation, finding points in neighboring segments, and building the grid DEM
Our Approach
We developed a new simple I/O-efficient algorithm for constructing a quad-tree based segmentation and storing the data structure on disk. Our algorithm also reports the points in segments neighboring each segment efficiently, and arranges the points on disk so that each segment can be interpolated in a simple scan over our data structure. Any interpolation method can be used with our segmentation scheme and a grid DEM can be efficiently computed using our approach.
Our Results
We implemented our algorithm and compared our implementation to existing interpolation methods. Previous implementations in both the commercial GIS ArcGIS and open-source GIS GRASS did not scale beyond 25 million points. Our approach scaled to points sets containing more than 390 million points and grid DEMs containing more than 1.3 billion cells.
Publication
P. Agarwal, L. Arge, and A. Danner. From Point Cloud to Grid DEM: A Scalable Approach. In Proc. International Symposium on Spatial Data Handling, 2006. pdf
Links
LIDAR fact sheet [pdf] from NC Floodmaps
LDART—NOAA
Coastal Services Center LIDAR Data Retrieval Tool
